資源の可採年数は一般に「静的可採年数」として「現有埋蔵量」を「年間消費量」で割ったものが用いられます。
(現有埋蔵量,ton)
(可採年数,y) = —————
(年間消費量,ton/y)
それぞれの個別の資源に関しては、この式で可採年数が得られますが、金属資源全体の傾向を知ろうとすると、生産量の大きな「鉄」の埋蔵量や生産量に引っ張られてしまいます。
そこで、金属元素それぞれを、使用している重量ではなく、資源の採掘に関わる「資源端」での量としてあらわすことで、重み付け平均を取りました。すなわち、ある資源を利用するために必要となる天然資源の量を「関与物質総量:TMR(Total Material Requirement)」と呼びますが、その1kgの資源に対する比率をi資源に対する「関与物質総量係数」Ciとして、それぞれの資源の現有埋蔵量と年間消費量それぞれにこの関与物質送料係数をかけて平均可採年数を求めています。
∑(関与物質総量係数Ci)(i資源の現有埋蔵量,ton)
(平均可採年数,y) = —————————————————–
∑ (関与物質総量係数Ci)(i資源の年間消費量,ton/y)
です。
これを経年で追いかけると下図のようになります。
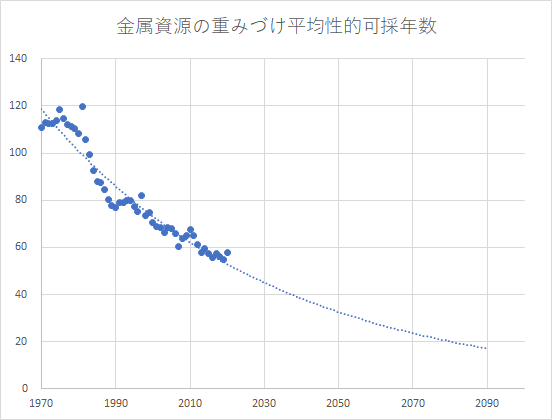
点線は希望的に指数近似で外挿を行ってみたものです。もし、1990-2020のデータをもとに直線近似外挿をすると。。。。
ただ、埋蔵量は「現在の技術とコストで採算性のある可採量で未可採のもの」というように、「コスト」の概念が入っていますので、金属価格が上昇すれば埋蔵量も増加します。ですから、埋蔵量がゼロになってしまうということは想定できないのですが、ということは、需要に対して可採年数が厳しくなれば、金属価格を高騰させて可採埋蔵量を確保していく、というメカニズムが働くことが予測されるというわけです。
元データ
埋蔵量、年間消費量: USGSwebサイト
関与物質総量係数 : 物質・材料研究機構 材料環境データ 「資源端量」