新型コロナウイルスの我が国での指数関数的増加

新型コロナウイルスの感染拡大が「指数関数的」と一般的に言われていますが、それを確認してみます。
まず、図は日経新聞4/11に出された、東京の新規患者数です。

日々患者数が増加していますが、3/25以降の増加は直線的に増加しているように見えます。こけれが指数関数的増加なのでしょうか。

ここで注意しなければならないのは、このグラフに書かれているのは新規の患者数であるということです。患者数をyとすると　この図にあらわされているのは、その増加速度vになります。

v= dx/dt の関係になるので。　もし　vが直線的に増加していたら、

v = a ・ t　+ b の関係になっているということで、
dy/dt = a・t + b よって
y=a・t² / 2+ b・t + const.

になります。これでは　二乗側にしかなりません。それは、「vが直線的に増加」と仮定したからで、目にはそう見えても目には気づかない異なった変化速度である可能性があります。

そういう時には、片対数のグラフを用います。

次の図は、日本の患者数のグラフです。これは累積患者数から累積退院数と累積死亡数を引いてあります。

患者数にしてみると、さすがに急速に増加しているのがわかります。しかし、これでは「指数関数的」すなわち鼠算の様に増えているのか、二乗則すなわち、単純加速度的に増えているのかは見極めら毛ません。これを片対数で表すと、より鮮明になります。

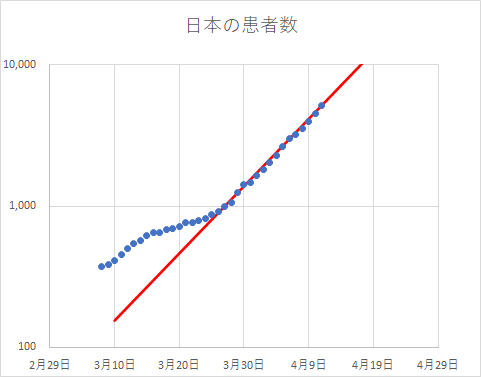
明らかにわかるように、3/25あたり以降からプロットが直線に乗っています。

ちなみに直線の加関係は

になっています。指数関数というと二倍、二倍という鼠算をイメージしますが、この場合は1日に0.05すなわち5%ずつ増えるという指数関数的増大で、毎日5%の複利が増殖しているというイメージになります。それでも、このペースのまま進めば、6月半ばには患者数は1億人に達する計算になります。
このような指数関数的な増大は、外出自粛が言われだした3/25あたりから始まっており、非常事態宣言後の現在も維持しています。非常事態宣言の効果はまだ出ていないということも言えますが、3/25もしくはその二週間前がどういう理由で指数関数的増加の出発点になったかということは、歴史が答えを出してくれると思います。

なお、指数関数的増加をより明確にチェックするには　増加速度　v=dy/dt と　患者数　yを両対数でプロットしてみることです。

次の図は、いくつかの国に対して、増加速度 v (=dy/dt) と　yを　プロットしたものです